How does temperature affect the gain of an SiPM?

Slawomir Piatek, PhD, Hamamatsu Corporation & New Jersey Institute of Technology
December 8, 2016

Introduction

A silicon photomultiplier (SiPM) is a solid-state photodetector capable of single-photon detection due to its high 10⁵ − 10⁷ internal gain (μ). Only one other photodetector, a photomultiplier tube (PMT), can achieve gain of such magnitude. Since its introduction in the mid-1990s, the SiPM has been undergoing a rapid development improving the performance. Compared to the first prototype, some undesirable characteristics such as high dark count rate density and high probability of optical crosstalk and of afterpulsing have been substantially reduced. These improvements, together with advantages over a PMT such as, to name a few, lower operating voltage, immunity to magnetic fields, and ruggedness, make a SiPM a viable alternative to a PMT as the detector for applications involving very low light levels. Many applications require stability of the photodetector's gain with respect to temperature changes. Fluctuating temperature can affect the gain of a PMT and SiPM; to prevent this, the photodetector operates either at a controlled constant temperature or at the ambient temperature but employing a gain-compensation circuitry. This technical note discusses the origin of the gain-temperature dependence in a SiPM and methods that the practitioner can use to correct for it.

Origin of the gain

A SiPM is a rectangular array of square microcells. Each microcell is composed of a series combination of an avalanche photodiode (APD) and a quenching resistor R_Q. All of the microcells are in parallel; thus, a SiPM has two terminals: anode and cathode. All of the APDs and quenching resistors are identical. To achieve high gain, the reverse bias V_BIAS applied to the SiPM exceeds the breakdown voltage V_BD of the APDs by up to several volts. Thus, the APDs operate in Geiger mode: once initiated, an avalanche would have been perpetual if it hasn't been quenched by an external (to the APD) circuitry, for example, R_Q. A SiPM is a current source: in response to a photon, the output is a current pulse i(t) and the gain equals the area under the pulse or $μ = \int_{0}^{\infty} i (t) d t$ . One can show that to an excellent approximation, μ is given by:

Equation 1

μ = \frac{(V_{B I A S} - V_{B D}) C_{J}}{e} = \frac{∆ V C_{J}}{e}

where ΔV is referred to as an "overvoltage," C_J is the capacitance of the APD's avalanche region and known as "junction capacitance," and e is the elementary charge. Equation 1 contains no explicit dependence on temperature, but there is an implicit dependence: it is well known that V_BD is a function of temperature, V_BD = V_BD(T). Additionally, one may not rule out the possibility that C_J can also vary with T. If V_BIAS is held constant, μ = μ(T) because ΔV = ΔV(T) and, possibly, C_J = C_J(T). The total derivative of μ with respect to T is given by:

Equation 2

\frac{d μ}{d T} = \frac{\partial μ}{\partial T} + \frac{\partial μ}{\partial ∆ V} \frac{d ∆ V}{d T} + \frac{\partial μ}{\partial C_{J}} \frac{d C_{J}}{d T}

Because there is no explicit dependence of μ on T, the first term on the right hand side of Equation 2 is zero. Using Equation 1 and assuming that V_BIAS is independent of T, after some rearranging, Equation 2 becomes:

Equation 3

\frac{d μ}{d T} = \frac{1}{e} (\frac{d C_{J}}{d T} ∆ V - \frac{d V_{B D}}{d T} C_{J})

Both ΔV and C_J are positive; therefore, the overall sign and magnitude of dμ/dT depends on the sign and magnitude of each term in the parentheses. The next paragraph discusses the first term.

Otte et al. (2016) is the most recent study to investigate how the key opto-electronic characteristics of a SiPM depend on T. It finds that C_J has a statistically insignificant correlation with T, as indicated by Figure 1 below.

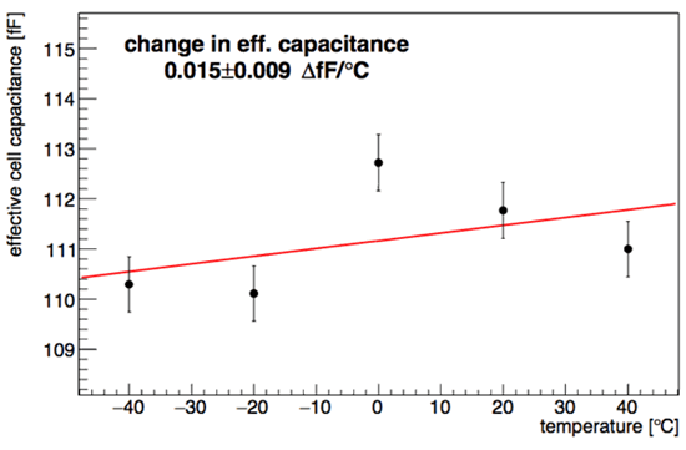
Figure 1. Dependence of junction capacitance on temperature for Hamamatsu S13360-3050CS SiPM. The figure is from Otte et al. (2016).

The best linear fit yields dC_J/dT = 0.015 ± 0.009 fF/°C. Taking C_J ≈ 111 fF from Figure 1, a one degree °C change in T causes a fractional change in C_J of about 0.014%. This change is small; thus, the first term in the parentheses of Equation 3 can be neglected, and C_J can be assumed constant in the second term. Therefore, the sign and magnitude of dμ/dT depends on how V_BD varies with T, as discussed next.

Otte et al. (2016) uses three different methods to determine the relationship between V_BD and T. All three methods indicate a linear dependence with nearly identical slopes as shown in Figure 2. The average slope, or dV_BD/dT, is about 55.7 mV/°C implying, according to Equation 3, that μ decreases linearly with T. For ΔV = 3 V, the one-degree °C change in T causes ~1.9% fractional change in ΔV — this is significant. The temperature-induced change of ΔV affects not only the gain but also other characteristics of a SiPM such as photon detection efficiency, dark count rate, crosstalk, and afterpulsing probability.

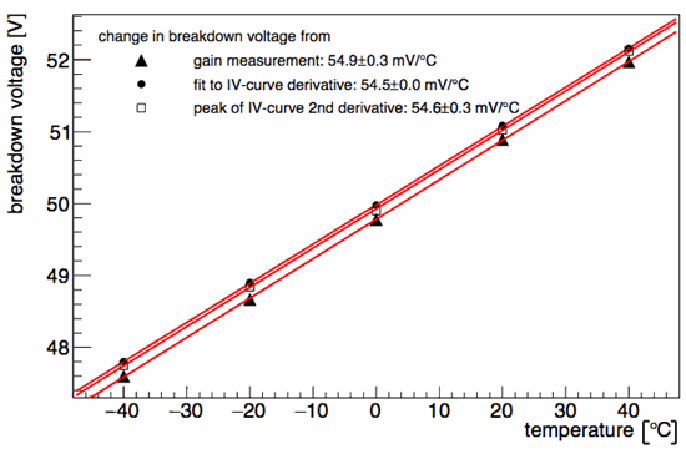
Figure 2. Dependence of breakdown voltage on temperature for Hamamatsu S13360-3050CS SiPM. The figure is from Otte et al. (2016).

Let β ≡ dV_BD/dT and express V_BD(T) = V_BD,0[1 + β(T - T₀)], where V_BD,0 is the breakdown voltage at the reference temperature T₀. The gain can now be written as:

Equation 4

μ (T) = \frac{C_{J}}{e} \{V_{B I A S} - V_{B D, 0} [1 + β (T - T_{0})]\} = \frac{C_{J}}{e} ∆ V (T)

To keep μ independent of T, ΔV(T) must be kept constant by adjusting V_BIAS to offset the change in V_BD. Namely:

Equation 5

V_{B I A S} = V_{B D, 0} + V_{B D, 0} β (T - T_{0})

A practical implementation of Equation 5 requires that β is known, that temperature can be accurately measured, and that a circuit with a temperature-voltage feedback loop can be constructed.

Practical implementation of gain control

Some manufacturers of SiPMs offer power supplies with built-in temperature compensation. Below is a view of a driver circuit (C12332-01) using a temperature-compensation power supply (C11204-01) by Hamamatsu.

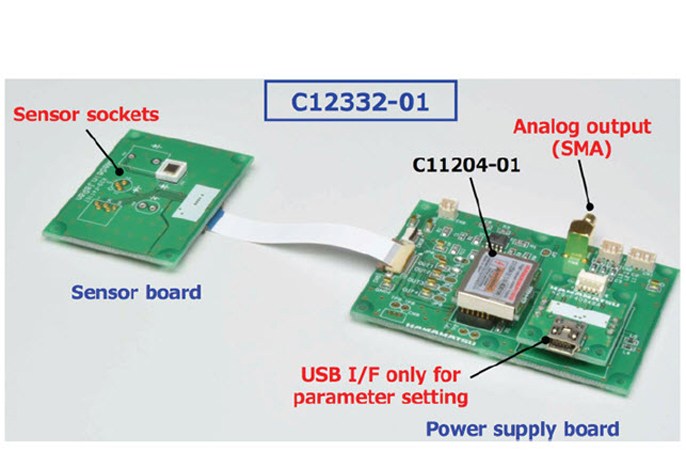
Figure 3. View of the Hamamatsu C12332-01 SiPM driver circuit with temperature compensation. The SiPM mounts in the sensor sockets of the sensor board.

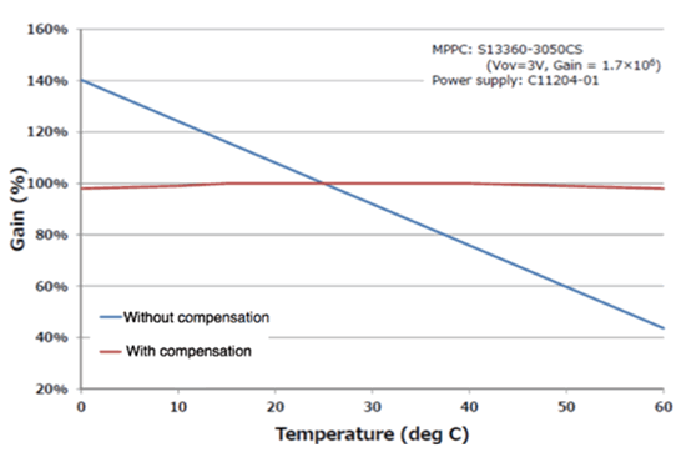
Figure 4. Gain variation versus temperature for Hamamatsu S13360-3050CS SiPM without temperature compensation (blue line) and with compensation (red line) provided by the C12332-01 driver circuit.

The SiPM is mounted on the "sensor board" containing the temperature sensor. Temperature information from the sensor goes to the "power supply board" where it is processed, and the feedback circuitry outputs the appropriate VBIAS to the SiPM. Figure 4 shows how the gain of Hamamatsu S13360-3050CS SiPM varies with temperature without temperature-compensation (blue line) and with temperature compensation (red line) provided by C12332-01.

The figure indicates that C12332-01 provides an excellent gain stabilization (gain variation less than about 2%) over at least a 60 °C temperature range.

Summary

For a fixed bias voltage, the gain of a SiPM changes linearly with temperature because the breakdown voltage varies linearly with temperature. Adjusting the bias voltage so that the overvoltage remains constant eliminates gain-temperature dependence. Manufacturers of SiPMs offer power supplies with a gain stabilization feature.

References

Otte, A. N., Garcia, D., Nguyen, T., Purushotham, D., Characterization of Three High Efficiency and Blue Sensitive Silicon Photomultipliers, Nuclear Inst. and Methods in Physics Research A, in press (2016)

Application notes

Automotive

Spectroscopy

Flow cytometry

Technical notes

Detector Selection

Image Sensors

PMTs

MPPC SiPMs

Spectrometers

Ask an engineer

Detectors

Distance measurement & LiDAR

Imaging

Infrared Products

Light sources

Optical components

Quantum technologies

Spectroscopy

Publications

Brochures

Research papers

Newsletter archives

United States (EN)

Select your region or country.

How does temperature affect the gain of an SiPM?

Introduction

Origin of the gain

Practical implementation of gain control

Summary

References

1. What are cookies?

2. What are the different types of cookies?

3. How do we use cookies?

4. Which cookies do we use?

5. What are Internet tags and how do we use them with cookies?

6. Analytics and Advertisement Cookies