Application notes
Technical notes
Ask an engineer
Publications
United States (EN)
Select your region or country.
What must be specified to achieve a valid spectroscopic measurement?
Professor Alexander Scheeline, PhD, University of Illinois Urbana-Champaign
May 3, 2016
Scientists and citizens often know what they want to measure in a specimen. Unfortunately, the specimen lacks their insight. Light and matter interact based on the rules of quantum and statistical mechanics, and humans interpret what happens based on their understanding of these rules. Wanting to make a measurement and making a valid measurement that contributes to the solution of a problem are thus not necessarily correlated.
The first requirement for a valid measurement is a representative sample which has been sufficiently characterized that the concomitants of the unknown are understood, interferences characterized, and thermal and chemical history adequately documented. One of the great illusions of analytical chemistry is to think that a measurement that works for pure samples in distilled water in a well-maintained laboratory will work well with any real world sample.1
Next, one must choose a measurement strategy. There are typically dozens of approaches to any measurement problem. Here, we will assume that one wishes to measure equilibrium absorbance in the ultraviolet (UV) (193 nm – 400 nm), visible (400 nm – 750 nm), or near-infrared (750 nm – 2500 nm) regions of the spectrum. How one decided not to use amperometry, Raman scattering, atomic emission, mass spectrometry, kinetics, or some chromatographic technique is not discussed. Even within the class of absorption measurements, one must decide between using a single (or narrow) range of wavelengths that is selective for the species of interest or a wide range of wavelengths within which one chemometrically extracts patterns that correlate with the sought-for quantity. Typically, selective absorption measurements are made in the UV or visible, pattern measurements in the near-infrared, but pattern measurements in the UV or visible are certainly possible. Narrow range measurements in the near-infrared are uncommon as distinct, selective features are rare. Figures 1A to 1C show cartoons of visible and near-infrared spectra, and examples of optical transitions of various widths.
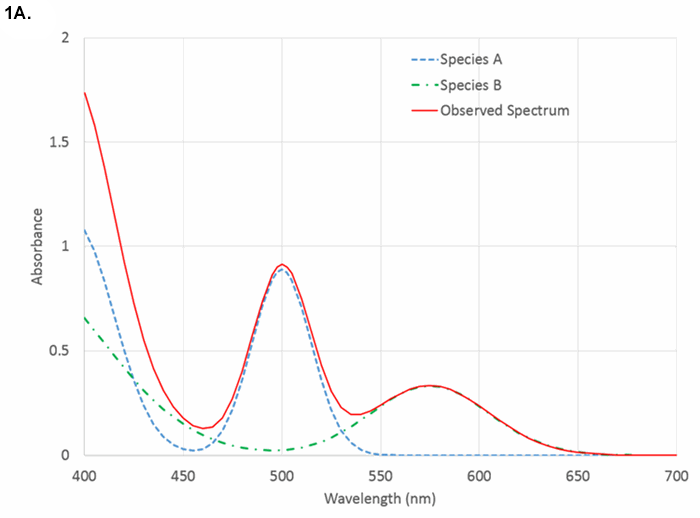
Figure 1A. Comparison of visible absorbance spectrum showing analyte-specific features.
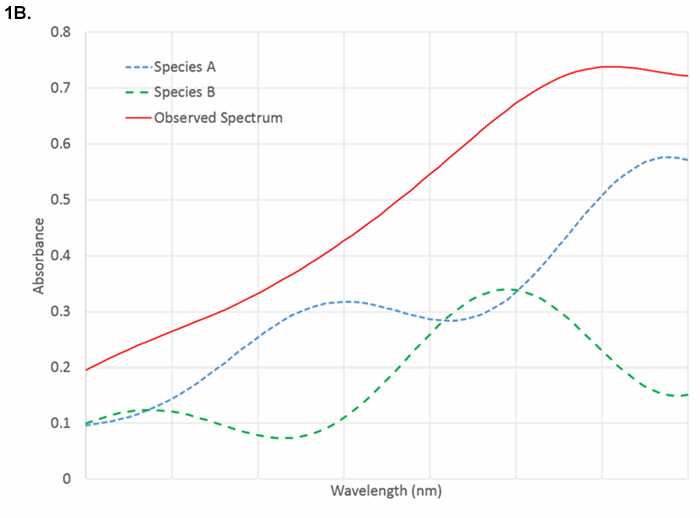
Figure 1B. Near-infrared spectra showing heavily overlapped spectra that require pattern recognition for quantification. Both species absorb at all wavelengths.
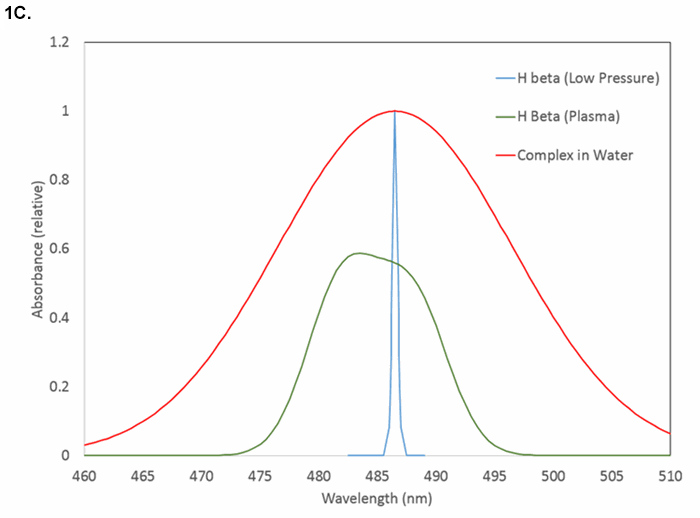
Figure 1C. Examples of line shapes and widths near 486 nm: hydrogen atomic emission at low electron density (narrowest), hydrogen atomic emission in dense plasma (intermediate), and molecular absorption (widest).
What spectral features selectively characterize the analyte?
Do the interferences produce phenomena at or near the same wavelength? How wide is the atomic or molecular transition? Atomic absorption lines have widths typically below 0.05 nm. Molecular absorption transitions in the visible and ultraviolet span ~10 - 50 nm with few exceptions (chromophores in the hydrophobic cores of proteins may be < 1 nm in width). Features in the near-infrared have widths from ~1 nm to hundreds of nanometers and are highly overlapped with absorbances from matrix materials and solvents.
What is the molar absorptivity of the analyte at its optimal wavelength?
What concentration is expected?
The Beer-Lambert Law that says absorbance is proportional to concentration applies for samples at low concentration where analyte molecules are individually solvated and do not noticeably perturb the solvent. The Law, Absorbance = pathlength times concentration times a scale factor (A=bCε) is deceptively simple. It assumes that one is looking at a single wavelength or a range of wavelengths over which the scale factor, the molar absorptivity, is constant. If ε = 50000 L mol-1 cm-1, in a 1 cm cuvette, one can typically measure A ~0.01 for quantitation of 0.2 μM analyte. What happens if the concentration is 1 mM? That is a factor of 5000 higher, leading to an extrapolation that A = 50. But that means that only one photon in 1050 would penetrate the sample, and there are likely fewer than 1020 s-1 to start with. Thus, the dynamic range of the measurement must be specified when choosing appropriate wavelengths. Of course the sample can be diluted to allow the measurement to proceed, but that requires awareness that A < 3 is typically desirable.
As concentrations change, molecular clusters may form, solvent structure may change, and refractive index, always a function of wavelength, may also change. Because the transmittance through an interface between media depends on the refractive index of both media, the transmitted signal depends on refraction as well as absorbance. Absorbance and refraction are connected by the Kramers-Krönig relationships,2,3 though data reduction that employs both absorbance and refraction is uncommon.
Suspended, scattering matter and refraction changes lead to baseline shifts and inaccurate measurements. In atomic absorption and infrared measurements, continuum radiation from instrument components (flames, furnaces, walls) are a source of stray light. Most commonly, one chooses a desired wavelength range and resolution, then hopes that scattering, stray light, and refraction are constants. Hope is a poor substitute for critical measurement.
The resolution needed from the instrument depends on the width of the spectral feature. Figures 2A and 2B show the observed absorbance compared to the absorbance in the middle of a Gaussian peak for various ratios of spectrometer width to feature width.
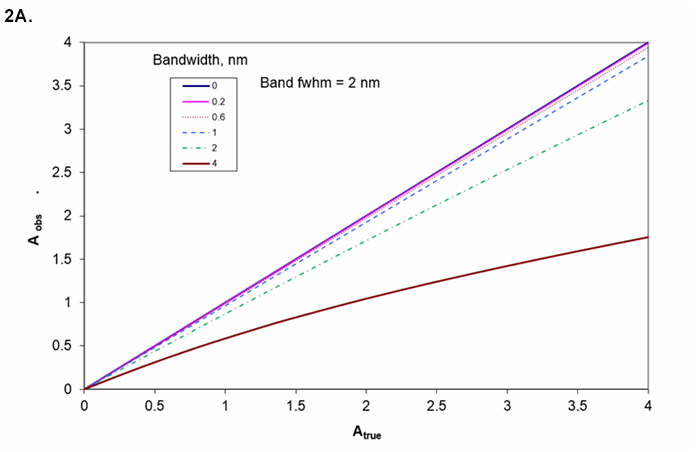
Figure 2A. Absorbance as a function of the ratio of spectrometer resolution to analyte line or bandwidth. Working curve curvature for various bandwidths if sample's bandwidth is 2 nm.
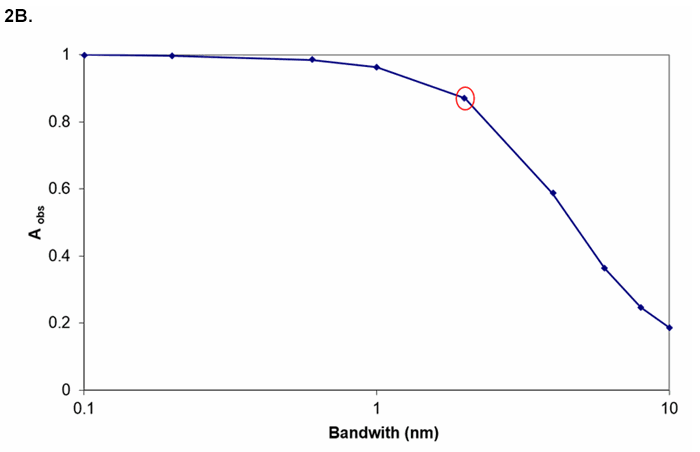
Figure 2B. Measured absorbance for true A = 1 for various bandwidths (transition bandwidth = 2 nm). If instrument bandwidth = transition bandwidth, A = 1 appears as A = 0.9.
How much light is available?
With too much light, absorbance transitions saturate and the amount of material is underestimated. With too little light, the measurement is noisy and results uncertain (about which more later). The energy absorbed by atoms or molecules is eventually, sometimes rapidly, released. This either raises the solvent temperature, gives rise to sample phosphorescence or fluorescence, or causes photochemical reaction. The branching ratio among these phenomena is typically difficult to control and is a function of the matrix. Changes in concomitants thus can alter the estimation of the amount of the analyte of interest, even in the absence of wavelength overlap with signals from the concomitants.
Separating light into its various wavelength, frequencies, or colors can be done in many ways. These include selection of a narrow band light source, filters, prisms, gratings, interferometers, selective detector response, and of course combinations. Interferometers have built-in wavelength references that monitor the scanning position of their movable mirrors and, for a given aperture (ratio of optics diameter to focal length), have better resolution than grating or prism spectrographs. In the infrared, interferometers give better precision than grating instruments because the major noise source is thermal noise in the detector (even when the detector is cooled) rather than in the rate of photon arrival. In the UV, in most instances, the particulate nature of light sets the noise floor. In the visible, photon arrival rate is also typically an important limiting factor. This gives rise to more frequent use of diffraction gratings and array detectors than interferometers in the UV, visible, and NIR.
The uncertainty in light intensity is a function of many physical and engineering choices, but with few exceptions if there are N photons detected, the highest possible signal-to-noise ratio is N1/2. The shorter the wavelength, the fewer photons there are per unit of energy, and the more important this "shot noise" is. Further, there is shot noise in background, stray light, and (in the case of multiwavelength detectors) adjacent wavelength regions. The precision of a result can be no better than the photometric precision. In addition to the number of detected photons, signals must be transduced to numbers. A precision of 1% corresponds to a signal-to-noise ratio of 100. This requires 104 photons. Readout resolution needs to be better than 1% so that any digitization errors do not overwhelm photon statistics errors. So the electronics should likely be configured to give 1 digitization count for every 10 photons. If we want to be able to measure at absorbance of 3 to a precision of 1%, then at 100% T we need 103 times 104 photons or 107 photons. The dynamic range then needs to be from 1 count for 10 photons to 106 counts for 107 photons. While some photomultipliers have a dynamic range of 106, few if any solid state array detectors have this broad range. Digitization is typically from 8 to 16 bits, but a factor of 106 equates to 20 bits. Yet, spectrometers with an absorbance range beyond 3 are widely available. How does this work? One way is to use detectors that can hold 216 electrons per pixel and then average many repetitive readouts from parallel pixels. A second way is to convert intensity to log(intensity) with analog circuitry and then digitize the logarithmic signal. In recent years, 20-bit analog-to-digital converters have become economically available, but they are of use only with the widest dynamic range detectors. Typical smartphone cameras and webcams only have 8-bit digitization per pixel. Is it any wonder that cameras optimized for selfies are rarely used for serious spectrometry? While averaging many 8-bit pixels together can give improved precision (1024 pixels gives 32 times the precision of a single pixel), the dynamic range of each pixel is only 1 part in 256. The author's research and business interests are focused on overcoming this limitation.4, 5, 6, 7
In the near-infrared, the wavelength range is wide enough and the shot noise low enough that interferometric energy sorting is common. Otherwise, interferometers are uncommon in this wavelength range. Prisms that double as lenses have been used in some instances, but diffraction gratings dominate wavelength dispersion in the UV and visible. Filters are employed either as low resolution, single wavelength, high throughput devices, or to select a subset of wavelengths more widely dispersed by gratings, or to block a narrow range of wavelengths (e.g., a laser when doing fluorescence or Raman scattering). All gratings suffer from order overlap; if one is looking at a specific diffraction angle, wavelengths appear with nλ, constant, where n is an integer and λ is a wavelength observable at that angle. Any other wavelength for which nλ has the same value will appear at the same position. Filters, light sources that only output over a narrow range of wavelengths, and energy-selective detectors are the common ways to overcome the ambiguities presented by order overlap.
Detectors can be single or multichannel, broadband or narrowband, and responsive to individual photons or total energy flux. At the lowest light levels, photomultipliers can be used to count the arrival of individual photons (although solid state SPADs, single-photon avalanche diodes, may also be employed), but the hunger for data parallelism has catalyzed the rise of array detectors. Silicon, whether fabricated into diode, CMOS, NMOS, or charge-coupled arrays, is responsive to light from ~400 nm to ~1100 nm, peaking in quantum efficiency (fraction of arriving photons giving rise to a signal) at ~900 nm. How can silicon arrays be used to sense light below 400 nm? A fluorophore is placed on the detector surface that absorbs in the ultraviolet and re-emits in the visible. Alternatively, since the 400 nm shortwave cutoff is due to absorbance by SiO rather than a falloff in response of silicon itself, one can use "backside-illuminated" arrays, where light hits the array on the side opposite the connecting leads, oxide is kept to one or a few monolayers, and ultraviolet photons can generate charge separation. NMOS, with negligible SiO coating thickness, inherently is sensitive across the ultraviolet. For wavelengths beyond 950 nm, one typically employs InGaAs, InAsSb, InSb, or InAs detectors.
All detectors provide some signal in the absence of illumination; this is the dark signal or dark current. Typically, it can be reduced by cooling the detector, but beyond some point, cooling also reduces photometric signal and leads to water vapor condensation on the detector and electronics. Shot noise in the dark current limits precision in measuring low light levels. On the other hand, cooling adds power demand and weight to the instrument. Does the detector need cooling? It depends on the amount of light, which in turn depends on the problem one is trying to solve.
High dispersion, typically a prerequisite for high resolution, spreads wavelengths widely across a focal plane. If dispersion is 10 nm/mm, the amount of light hitting a detector of a given size is 10 times higher than if dispersion is 1 nm/mm, all else equal. In light-limited situations, minimizing dispersion is necessary for adequate precision. Conversely, if there is too much light, one may either use higher dispersion, narrow entrance apertures, or less responsive detectors to allow measurements to be made. Interestingly, for atomic absorption, fairly low dispersion spectrometers are common. The narrow atomic emission in a hollow cathode discharge tube, emitting light only for the element of interest and of a rare gas used to support the discharge plasma in the lamp, provides the high resolution portion of the selectivity, while the spectrograph acts mostly as a filter to keep distant lines of either the discharge gas or element of interest from generating stray light.
Once data are in hand, it is tempting to simply run it through Beer's Law, do a linear fit to the data, use that fit as a working curve, and crank out results. However, critical evaluation of the data and the results is usually essential. The ability to see if unexpected absorbances or baseline shifts have occurred is one of the strengths of array detector instruments. Comparison of signal levels with those typical of a given class of specimens allows detection of improper sample preparation, unexpectedly low (or high) light levels, unexpected chemical interactions, unexpected pH shifts, and so on. Just because it's a number from a computer doesn't make it right! Even greater care is required when pattern recognition is employed. Any variation in illumination, detector temperature, optical alignment, or specimen contaminants can give rise to numerically accurate, technically flawed results. Pattern recognition works best with carefully controlled instruments whose condition is confirmed frequently with control samples. One can throw numbers into any pattern recognition algorithm, and something will always be recognized, even if none of the calibration materials are present.
So how can one choose an instrument?
A first pass is shown in Figure 3. After choosing a class of instrument and detector, one then has to choose a specific model. Each has particular wavelength range, resolution, signal-to-noise ratio under some set of conditions, flexibility in sample handling, light source brightness and lifetime, readout speed in pixels per second or spectra per second, integration time per pixel or per readout cycle, intensity dynamic range, and dark current. To keep the diagram from looking like a bowl of spaghetti, an important aspect has been omitted: after a set of choices have been made, one must validate the measurements with known specimens. If performance is inadequate, the source of the inadequacy must be tracked down and then different choices made to circumvent the limitations of the original approach. One iterates to an acceptable compromise among information obtained, resilience to variations in sample concomitants and measurement environment, response speed, and cost.
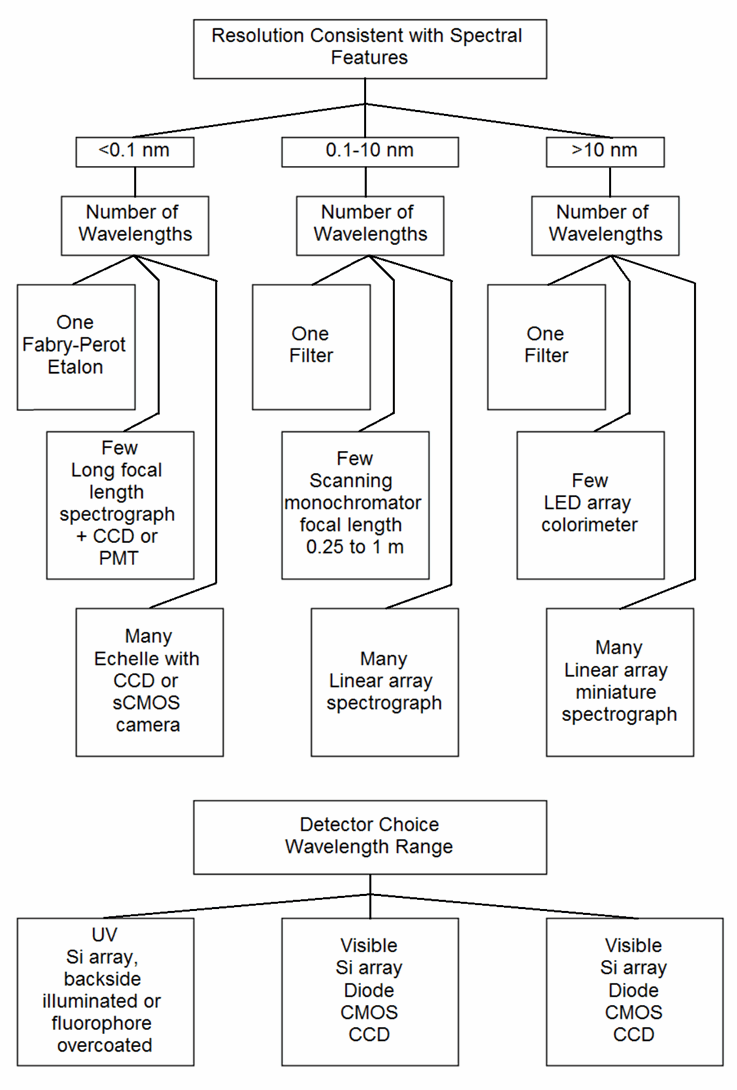
Figure 3. Partial flowchart for selecting methods and parameters
As one example, an instrument with 0.1% precision in the lab that weighs 20 kg is useless for measurements to be made 30 km into the wilderness where no power (except perhaps a 20 kg battery pack) is available and where temperature can change in minutes. Similarly, a portable instrument with 5% precision is inadequate for assays of pharmaceuticals where dosage and contaminants need to be tightly controlled and any unexpected absorbance from undocumented components are unacceptable.
A second example involves detector choice. Just among rectangular CMOS arrays, full well capacity per pixel may range from 6000 electrons to 70,000 electrons. Silicon array detectors in general may range from 6000 electrons to 5 x 108 electrons, nearly 5 orders of magnitude (though the storage capacity of Si is approximately 10,000 electrons per square micron for all the devices).
The resolution realizable for each detector depends not only on pixel dimensions but also on the dispersion of the spectrometer to which they are attached, further complicating estimation of the resolution, precision, and wavelength range tradeoffs. If a measurement would require integration over an excessive period of time, an alternative choice is in order.
With all these choices, instrument selection can be confusing. So take a deep breath, and write down what problem or set of problems you are trying to solve. If the problems have contradictory demands, one instrument alone won't do the job. The less demanding one is of precision and accuracy, the more generally applicable can be the chosen instrument. After all, if one is looking at, e.g., water quality, the simplest instrument costs nothing at all! Just look at the water through a clear container. "Looks clear" doesn't prove it's drinkable, but "yuck!" likely indicates it is not. To get more precise requires instrumentation and sample preparation, and the more precise one wishes to be, the more demanding both the sample preparation and instrument selection is required.
References
- G. E. F. Lundell, "The Chemical Analysis of Things as They Are," Industrial and Engineering Chemistry, Analytical Edition, vol. 5, no. 4, pp. 221–225, 1933.
- B. J. Davis, P. S. Carney, and R. Bhargava, "Theory of Mid-infrared Absorption Microspectroscopy: II. Heterogeneous Samples," Analytical Chemistry, vol. 82, no. 9, pp. 3487–3499, May 2010.
- B. J. Davis, P. S. Carney, and R. Bhargava, "Theory of Mid–infrared Absorption Microspectroscopy: I. Homogeneous Samples," Analytical Chemistry, vol. 82, no. 9, pp. 3474–3486, May 2010.
- A. Scheeline and T. A. Bui, "Stacked, Mutually-rotated Diffraction Gratings as Enablers of Portable Visible Spectrometry," Applied Spectroscopy, vol. 70, no. 5, 2016.
- A. Scheeline and T. A. Bui, "Energy Dispersion Device," U.S. patent 8,885,161, 2014.
- A. Scheeline, "Focal Point: Teaching, Learning, and Using Spectroscopy with Commercial, Off-the-Shelf Technology," Applied Spectroscopy, vol. 64, no. 9, p. 256A–268A, 2010.
- A. Scheeline, "Is 'Good Enough' Good Enough for Portable Visible and Near-Visible Spectrometry?," in Next-Generation Spectroscopic Technologies VIII, 2015, pp. 94820H–1 – 94820H–9.
About the author
Alexander Scheeline, PhD, is Professor Emeritus, Department of Chemistry, University of Illinois Urbana-Champaign. Dr. Scheeline is also President of SpectroClick Inc. and an honorary member of the Society for Applied Spectroscopy.
- Confirmation
-
It looks like you're in the . If this is not your location, please select the correct region or country below.
You're headed to Hamamatsu Photonics website for US (English). If you want to view an other country's site, the optimized information will be provided by selecting options below.
In order to use this website comfortably, we use cookies. For cookie details please see our cookie policy.
- Cookie Policy
-
This website or its third-party tools use cookies, which are necessary to its functioning and required to achieve the purposes illustrated in this cookie policy. By closing the cookie warning banner, scrolling the page, clicking a link or continuing to browse otherwise, you agree to the use of cookies.
Hamamatsu uses cookies in order to enhance your experience on our website and ensure that our website functions.
You can visit this page at any time to learn more about cookies, get the most up to date information on how we use cookies and manage your cookie settings. We will not use cookies for any purpose other than the ones stated, but please note that we reserve the right to update our cookies.
1. What are cookies?
For modern websites to work according to visitor’s expectations, they need to collect certain basic information about visitors. To do this, a site will create small text files which are placed on visitor’s devices (computer or mobile) - these files are known as cookies when you access a website. Cookies are used in order to make websites function and work efficiently. Cookies are uniquely assigned to each visitor and can only be read by a web server in the domain that issued the cookie to the visitor. Cookies cannot be used to run programs or deliver viruses to a visitor’s device.
Cookies do various jobs which make the visitor’s experience of the internet much smoother and more interactive. For instance, cookies are used to remember the visitor’s preferences on sites they visit often, to remember language preference and to help navigate between pages more efficiently. Much, though not all, of the data collected is anonymous, though some of it is designed to detect browsing patterns and approximate geographical location to improve the visitor experience.
Certain type of cookies may require the data subject’s consent before storing them on the computer.
2. What are the different types of cookies?
This website uses two types of cookies:
- First party cookies. For our website, the first party cookies are controlled and maintained by Hamamatsu. No other parties have access to these cookies.
- Third party cookies. These cookies are implemented by organizations outside Hamamatsu. We do not have access to the data in these cookies, but we use these cookies to improve the overall website experience.
3. How do we use cookies?
This website uses cookies for following purposes:
- Certain cookies are necessary for our website to function. These are strictly necessary cookies and are required to enable website access, support navigation or provide relevant content. These cookies direct you to the correct region or country, and support security and ecommerce. Strictly necessary cookies also enforce your privacy preferences. Without these strictly necessary cookies, much of our website will not function.
- Analytics cookies are used to track website usage. This data enables us to improve our website usability, performance and website administration. In our analytics cookies, we do not store any personal identifying information.
- Functionality cookies. These are used to recognize you when you return to our website. This enables us to personalize our content for you, greet you by name and remember your preferences (for example, your choice of language or region).
- These cookies record your visit to our website, the pages you have visited and the links you have followed. We will use this information to make our website and the advertising displayed on it more relevant to your interests. We may also share this information with third parties for this purpose.
Cookies help us help you. Through the use of cookies, we learn what is important to our visitors and we develop and enhance website content and functionality to support your experience. Much of our website can be accessed if cookies are disabled, however certain website functions may not work. And, we believe your current and future visits will be enhanced if cookies are enabled.
4. Which cookies do we use?
There are two ways to manage cookie preferences.
- You can set your cookie preferences on your device or in your browser.
- You can set your cookie preferences at the website level.
If you don’t want to receive cookies, you can modify your browser so that it notifies you when cookies are sent to it or you can refuse cookies altogether. You can also delete cookies that have already been set.
If you wish to restrict or block web browser cookies which are set on your device then you can do this through your browser settings; the Help function within your browser should tell you how. Alternatively, you may wish to visit www.aboutcookies.org, which contains comprehensive information on how to do this on a wide variety of desktop browsers.
5. What are Internet tags and how do we use them with cookies?
Occasionally, we may use internet tags (also known as action tags, single-pixel GIFs, clear GIFs, invisible GIFs and 1-by-1 GIFs) at this site and may deploy these tags/cookies through a third-party advertising partner or a web analytical service partner which may be located and store the respective information (including your IP-address) in a foreign country. These tags/cookies are placed on both online advertisements that bring users to this site and on different pages of this site. We use this technology to measure the visitors' responses to our sites and the effectiveness of our advertising campaigns (including how many times a page is opened and which information is consulted) as well as to evaluate your use of this website. The third-party partner or the web analytical service partner may be able to collect data about visitors to our and other sites because of these internet tags/cookies, may compose reports regarding the website’s activity for us and may provide further services which are related to the use of the website and the internet. They may provide such information to other parties if there is a legal requirement that they do so, or if they hire the other parties to process information on their behalf.
If you would like more information about web tags and cookies associated with on-line advertising or to opt-out of third-party collection of this information, please visit the Network Advertising Initiative website http://www.networkadvertising.org.
6. Analytics and Advertisement Cookies
We use third-party cookies (such as Google Analytics) to track visitors on our website, to get reports about how visitors use the website and to inform, optimize and serve ads based on someone's past visits to our website.
You may opt-out of Google Analytics cookies by the websites provided by Google:
https://tools.google.com/dlpage/gaoptout?hl=en
As provided in this Privacy Policy (Article 5), you can learn more about opt-out cookies by the website provided by Network Advertising Initiative:
http://www.networkadvertising.org
We inform you that in such case you will not be able to wholly use all functions of our website.
Close